Two View Geometry

Planar 2D-2D Geometry (Projective Geometry)

---

Overview of Perspective Geometry

• Planar Homography Estimation

  

  • Unknown
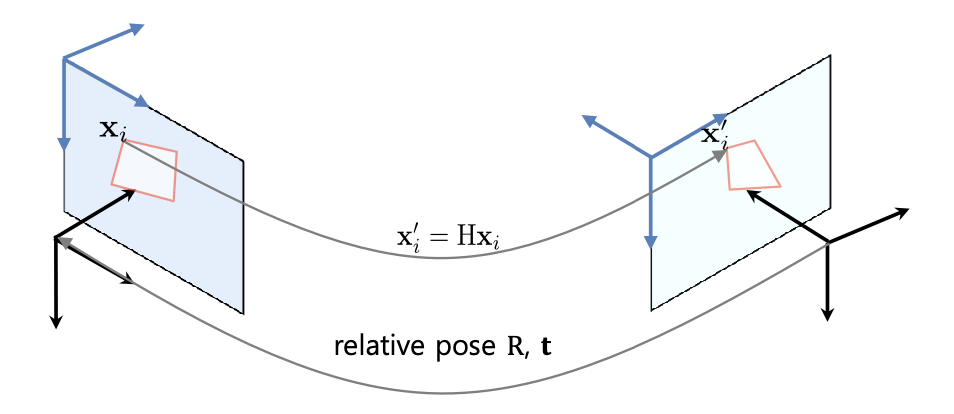
    • Planar homography (8 DoF)
  • Given
    • Point correspondence $\left(\mathbf{x}{1}, \mathbf{x}{1}^{\prime}\right), \ldots,\left(\mathbf{x}{n}, \mathbf{x}{n}^{\prime}\right)$
  • Constraints
    • $n \times \text { projective transformation } \mathbf{x}{i}^{\prime}=\mathrm{H} \mathbf{x}{i}$
  • Solutions ($n \geq 4$) ⇒ 4-point algorithm
    • OpenCV cv::getPerspectiveTransform() and cv::findHomography()

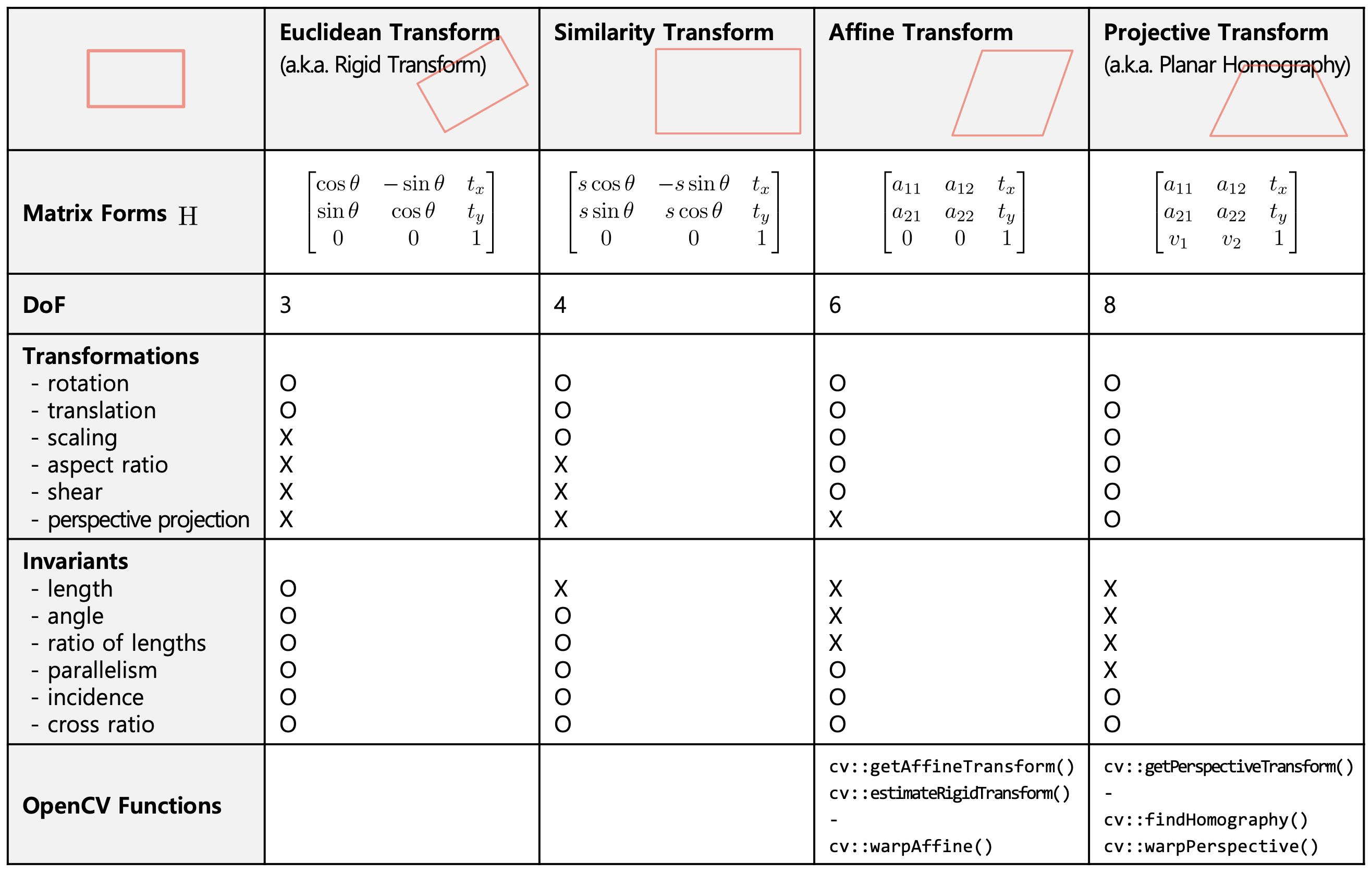
    • cf. More simplified transformations need less number of minimal correspondence.

      → Affine ($n \geq 3$), similarity ($n \geq 2$), Euclidean ($n \geq 2$)

  • [Note] Planar homography can be decomposed as relative camera pose.
    • OpenCV cv::decomposeHomographyMat()
    • cf. However, the decomposition needs to know camera matrices.

General 2D-2D Geometry (Epiploar Geometry)

---

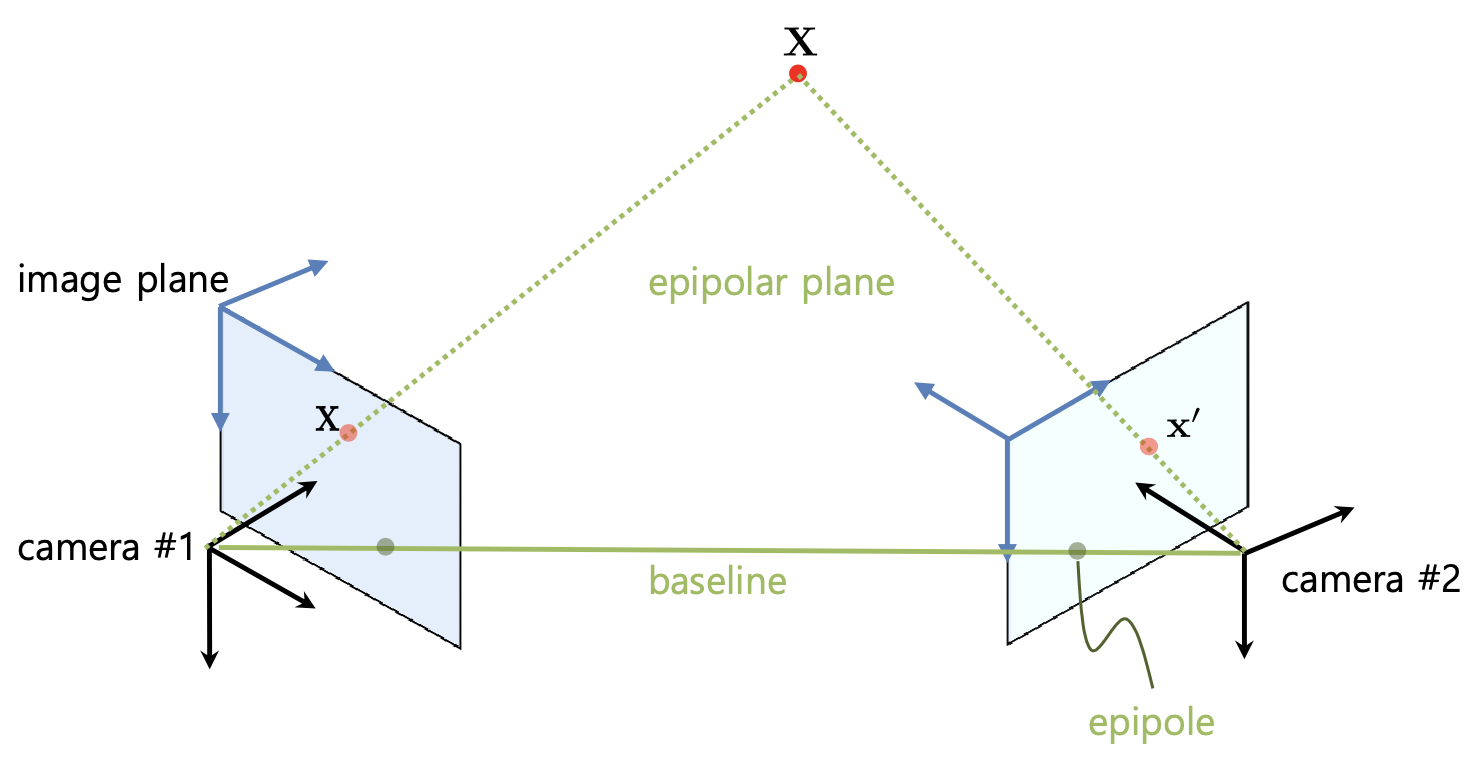
Overview of Epipolar Geometry

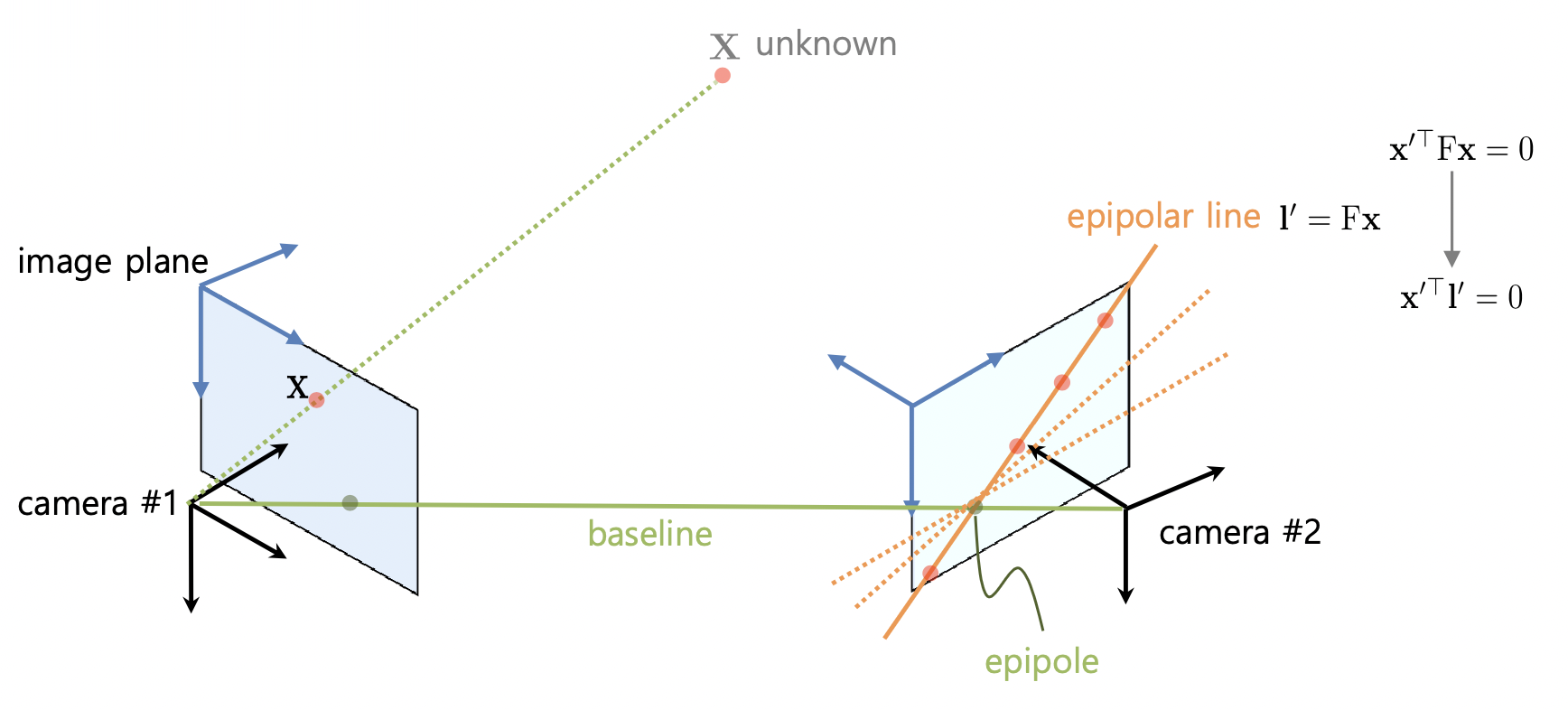
Fundamental Matrix

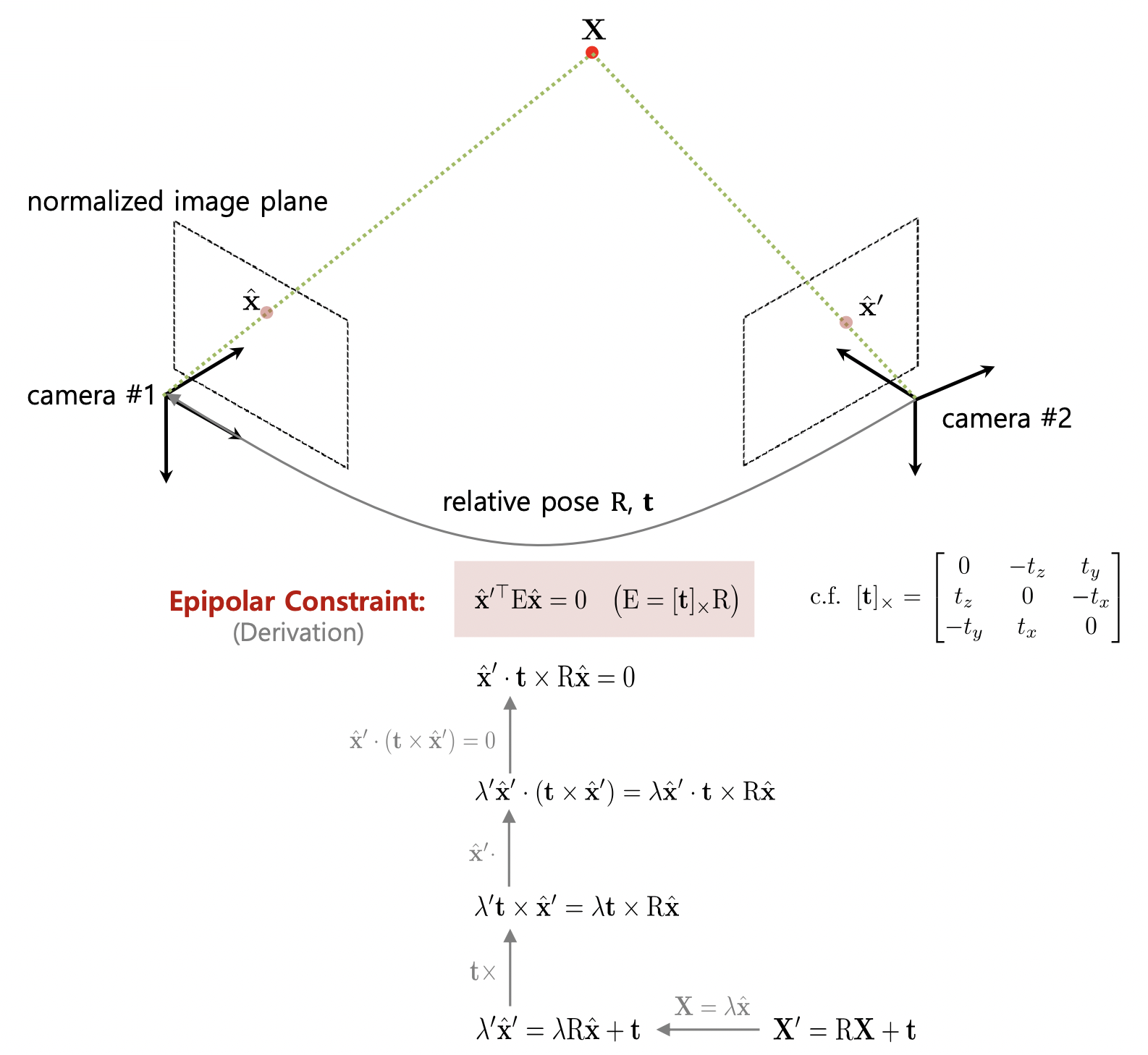
Essential Matrix

Epiplar Geometry

• Relative Camera Pose Estimation (~ Fundamental/Essential Matrix Estimation)

  

  • Unknown
    • Rotation and translation $\mathrm{R,t}$ (5 DoF; up-to scale “scale ambiguity”)
  • Given
    • Point correspondence $\left(\mathbf{x}_1, \mathbf{x}_1^{\prime}\right), \ldots,\left(\mathbf{x}_n, \mathbf{x}_n^{\prime}\right)$
    • camera matrices $\mathrm{K,K’}$
  • Constraints
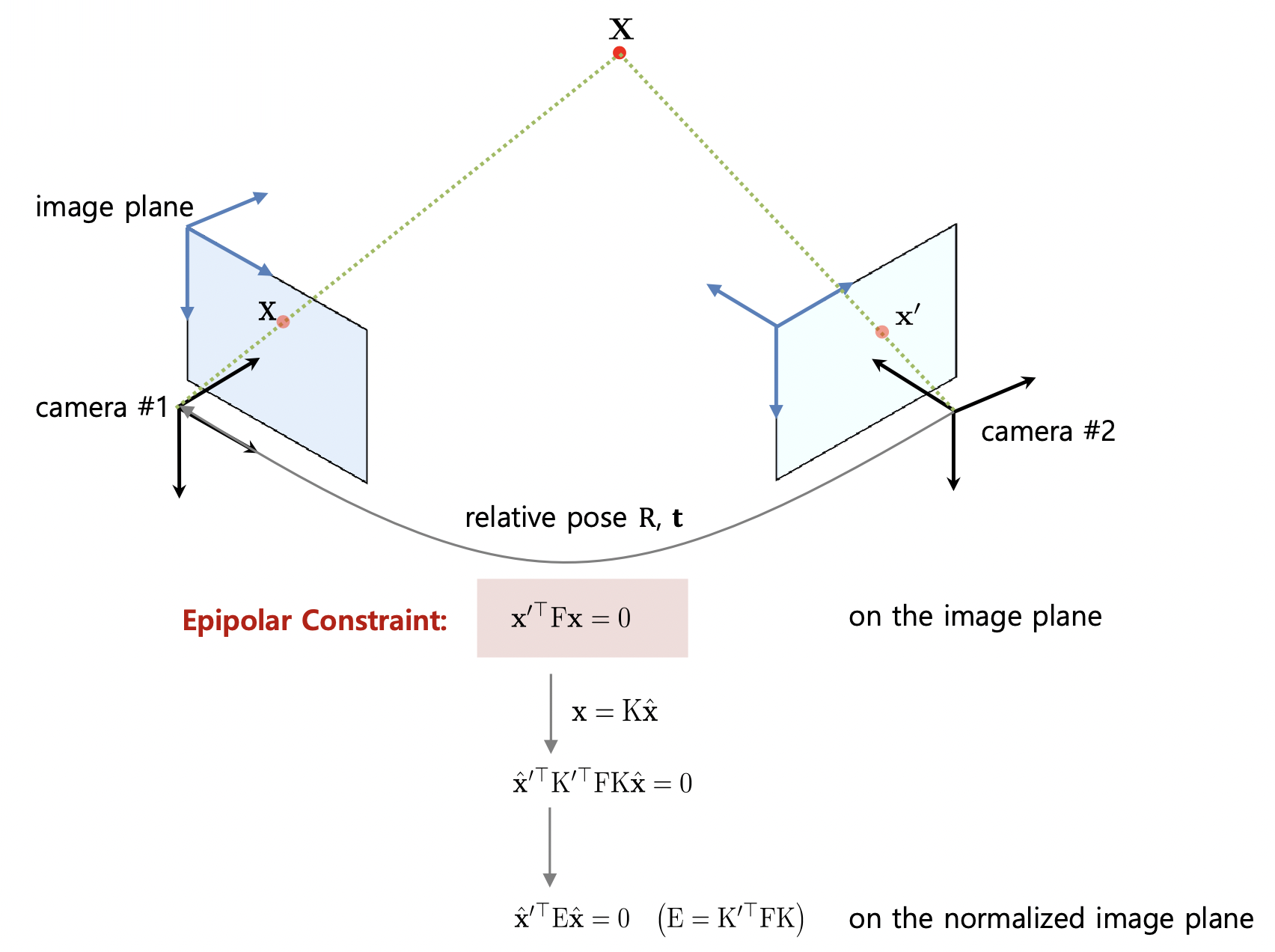
    • $n \times \text { epipolar constraint }\left(\mathbf{x}^{\prime \top} \mathrm{F} \mathbf{x}=0 \text { or } \hat{\mathbf{x}}^{\prime \top} \mathrm{E} \hat{\mathbf{x}}=0\right)$
  • Solutions (OpenCV)

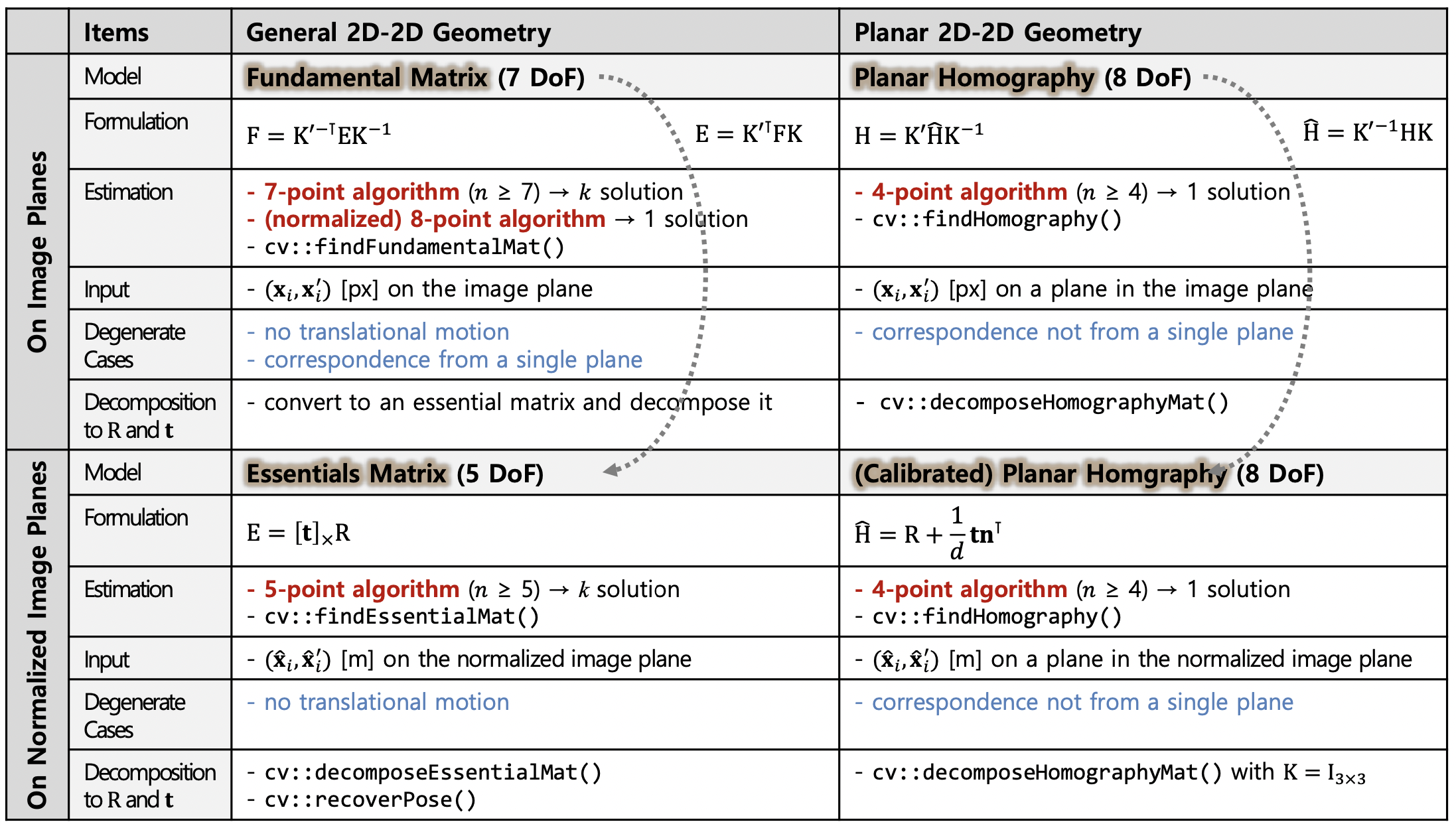
    • Fundamental matrix: 7/8-point algorithm (7 DoF)

      → Estimation: cv::findFundamentalMat() ⇒ 1 solution

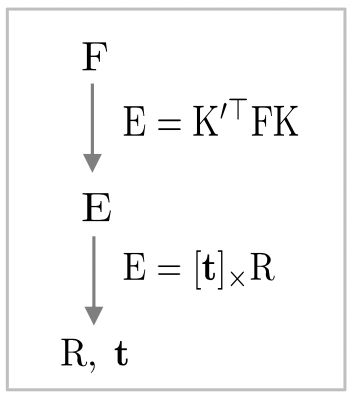
      → Conversion to $\mathrm{E}$: $\mathrm{E}=\mathrm{K}^{\prime \top} \mathrm{FK}$

      → Degenerate cases: No translation, correspondence from a single plane

      → intrinsic & extrinsic camera parameters

    • Essential matrix: 5-point algorithm (5 DoF)

      → Estimation: cv::findEssentialMat() ⇒ $k$ solutions

      → Decomposition: cv::decomposeEssentialMat() ⇒ 4 solutions “relative pose ambiguity”

      → Decomposition with positive-depth check: cv::recoverPose() ⇒ 1 solution

      → Degenerate case: No translation ($\because \mathrm{E}=[\mathrm{t}]_{\times} \mathrm{R}$)

      → extrinsic camera parameters

    • Planar homography: 4-point algorithm (8 DoF)

      → Estimation: cv::findHomography() ⇒ 1 solution

      → Conversion to calibrated $\mathrm{H}$: $\widehat{\mathrm{H}}=\mathrm{K}^{\prime-1} \mathrm{HK}$ → Decomposition: cv::decomposeHomographyMat() ⇒ 4 solutions → Degenerate case: Correspondence not from a single plane

      → intrinsic & extrinsic camera parameters + plane normal

본 포스트는 최성록 교수님의 An Inviation to 3D Vision 자료를 정리한 것입니다.