Multiview Geometry

Multi-view Geometry

Bundle Adjustment

• Unknown
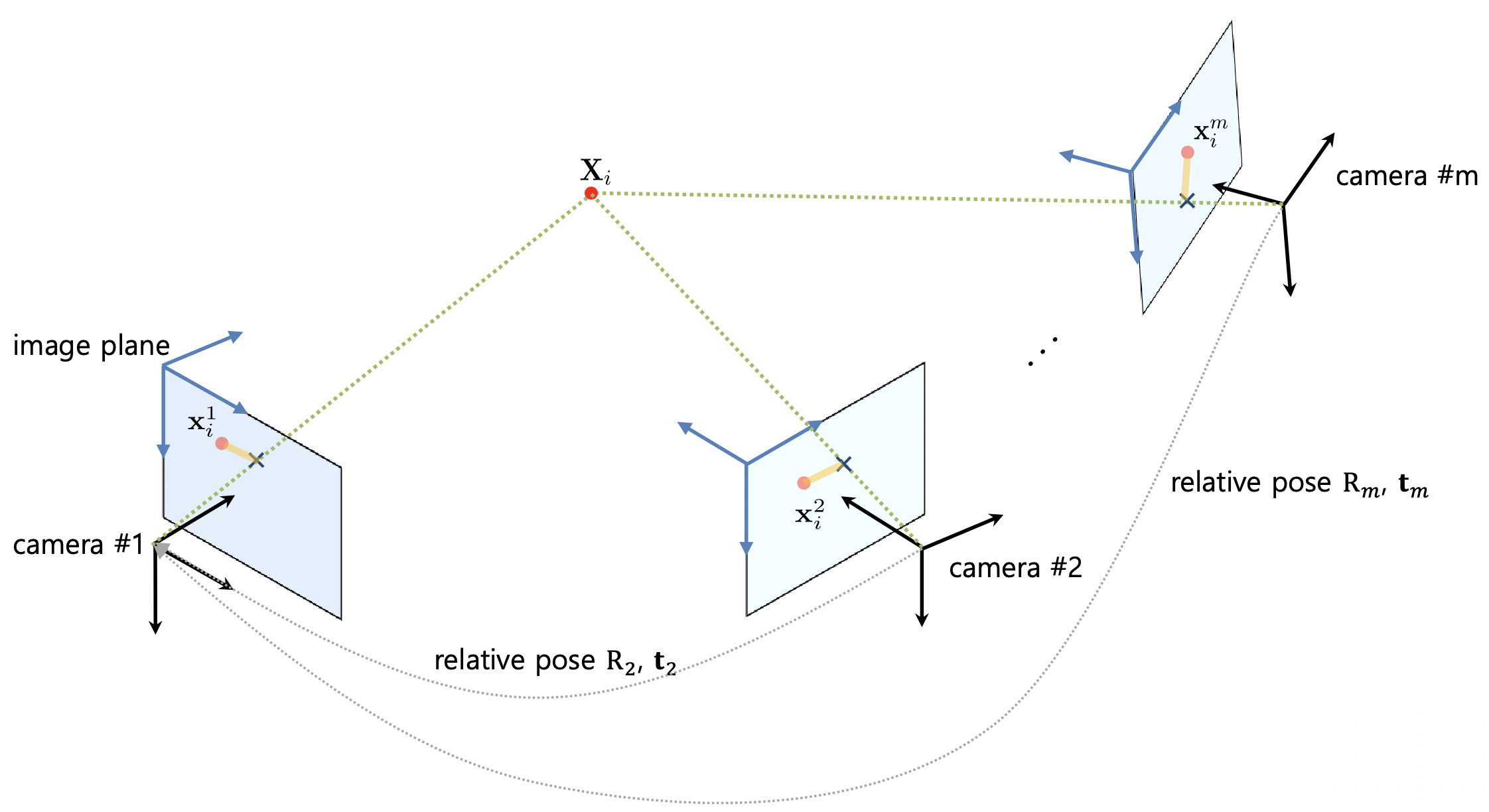
  • Position of 3D points and each camera’s relative pose ($6n+3m$ DoF)
• Given
  • Point correspondence
  • camera matrices
  • position of 3D points
  • each camera’s relative pose
• Constraints
  • $n \times m \times \text { projection } \mathbf{x}_i^j=\mathrm{P}_j \mathbf{X}_i=\mathrm{K}_j\left[\mathrm{R}_j \mid \mathbf{t}_j\right] \mathbf{X}_i$
• Solution ⇒ Non-linear least-square optimization
  • Cost Function

    • Reprojection error

      $\sum\limits_i^n \sum\limits_j^m v_i^j\left|\mathbf{x}i^j-\mathrm{P}_j \mathbf{X}_i\right|{\Sigma}^2 \quad \text { where } \quad v_i^j= \begin{cases}1 & \text { if } \mathbf{x}_i^j \text { is visible } \ 0 & \text { otherwise }\end{cases}$

  • Optimization
    • Levenberg–Marquardt method
    • Gauss-Newton method

Bundle Adjustment and Optimization Tools

• OpenCV
  • No function (but cvsba is available as a sba wrapper.)
• Bundle adjustment
  • sba (Sparse Bundle Adjustment)
  • SSBA (Simple Sparse Bundle Adjustment)
  • pba (Multicore Bundle Adjustment)
• (Graph) Optimization
  • g2o (General Graph Optimization)
  • iSAM (Incremental Smoothing and Mapping)
  • GTSAM
  • Ceres Solver (Google)

Applications

---

Structure-from-motion

• SfM (Global)

  1. Build a viewing graph (well-matched pairs) while finding inliers

     ⇒ Load images and extract features

     ⇒ Match features and find good matches (which has enough inliers)

     

  2. Initialize cameras ($R, t, f, …$)
  3. Initialize 3D points and build a visibility graph

  4. Optimize camera pose and 3D points together (BA)

     

• SfM (Incremental)
  • Incrementally add more views
  • repeat 4~7
    1. Build a viewing graph (well-matched pairs) while finding inliers
    2. Select the best pair
    3. Estimate relative pose from the best two views (epipolar geometry)
    4. Reconstruct 3D points of the best two views (triangulation)
    5. Select the next image to add

    ⇒ Separate points into known and unknown for PnP (known) and triangulation (unknown)

  1. Estimate relative pose of the next view (PnP)
  2. Reconstruct newly observed 3D points (triangulation)
  3. Optimize camera pose and 3D points together (BA)

  

Visual SLAM

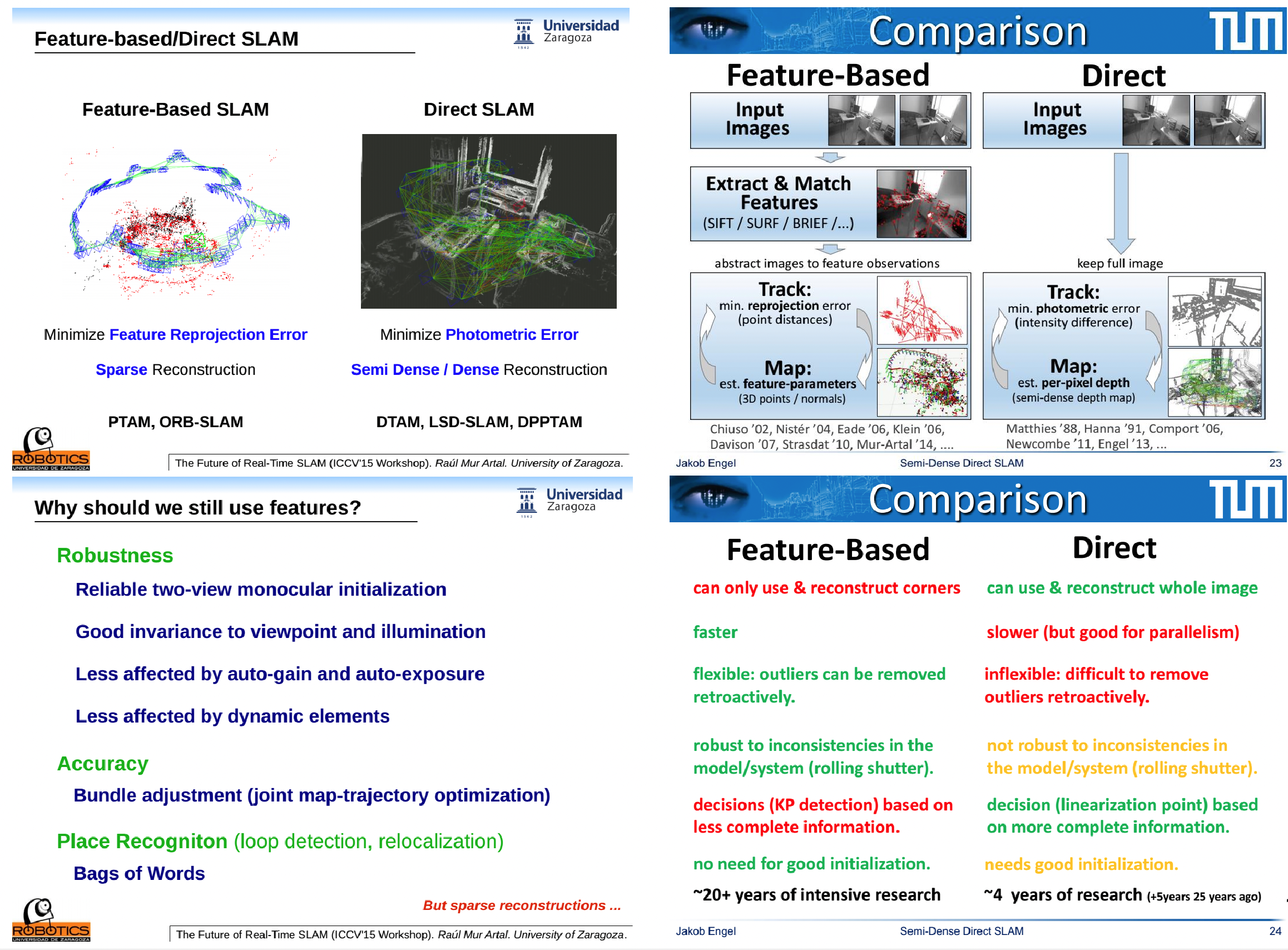
• Feature-based Method vs Direct Method

  

  

Visual Odometry

• Visual Odometry vs Wheel Odometry

  Visual Odometry	Wheel Odometry
  + direct motion measure	+ simple calculation
  + six degree-of-freedoms
  + easy to install
  − heavy computation	− indirect motion measure (e.g. slippage)
  − visual disturbance (e.g. moving objects)	− two degree-of-freedoms
  	− necessary to be on rotor/shaft

• Visual Odometry vs Visual SLAM
  • Visual Odometry

    • no assumption on trajectories

      ⇒ navigation / large space (outdoor)

  • Visual SLAM

    • closed-loop is preferred for convergence

      ⇒ mapping / small space (indoor, campus)

• Feature-based Monocular Visual Odometry

  • Two-view Motion Estimation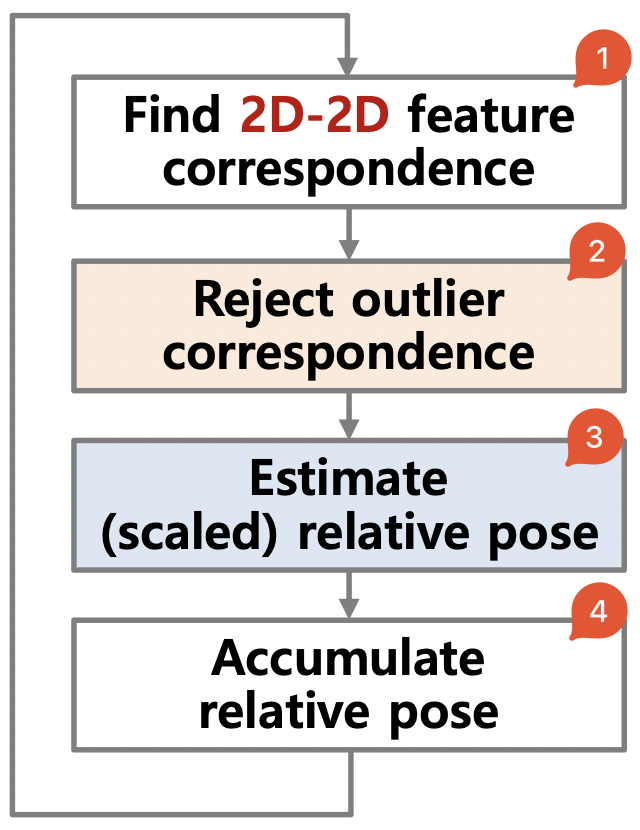

    

    1. Find 2D-2D feature correspondence

       • Feature

         → Good-Feature-to-Track [Shi94_CVPR] with bucketing to distribute features

       • Correspondence

         → Lucas-Kanade optical flow [Lucas81_IJCAI]

    2. Reject outlier correspondence
       • Adaptive MSAC [Choi09_IROS]
       • Iterative 5-point algorithm [Choi15_IJCAS]

       • Error measure

         → Sampson distance

    3. Estimate (scaled) relative pose
       • Normalized 8-point algorithm
       • Scale-from-ground with asymmetric kernels [Choi13_URAI]

  • PnP Pose Estimation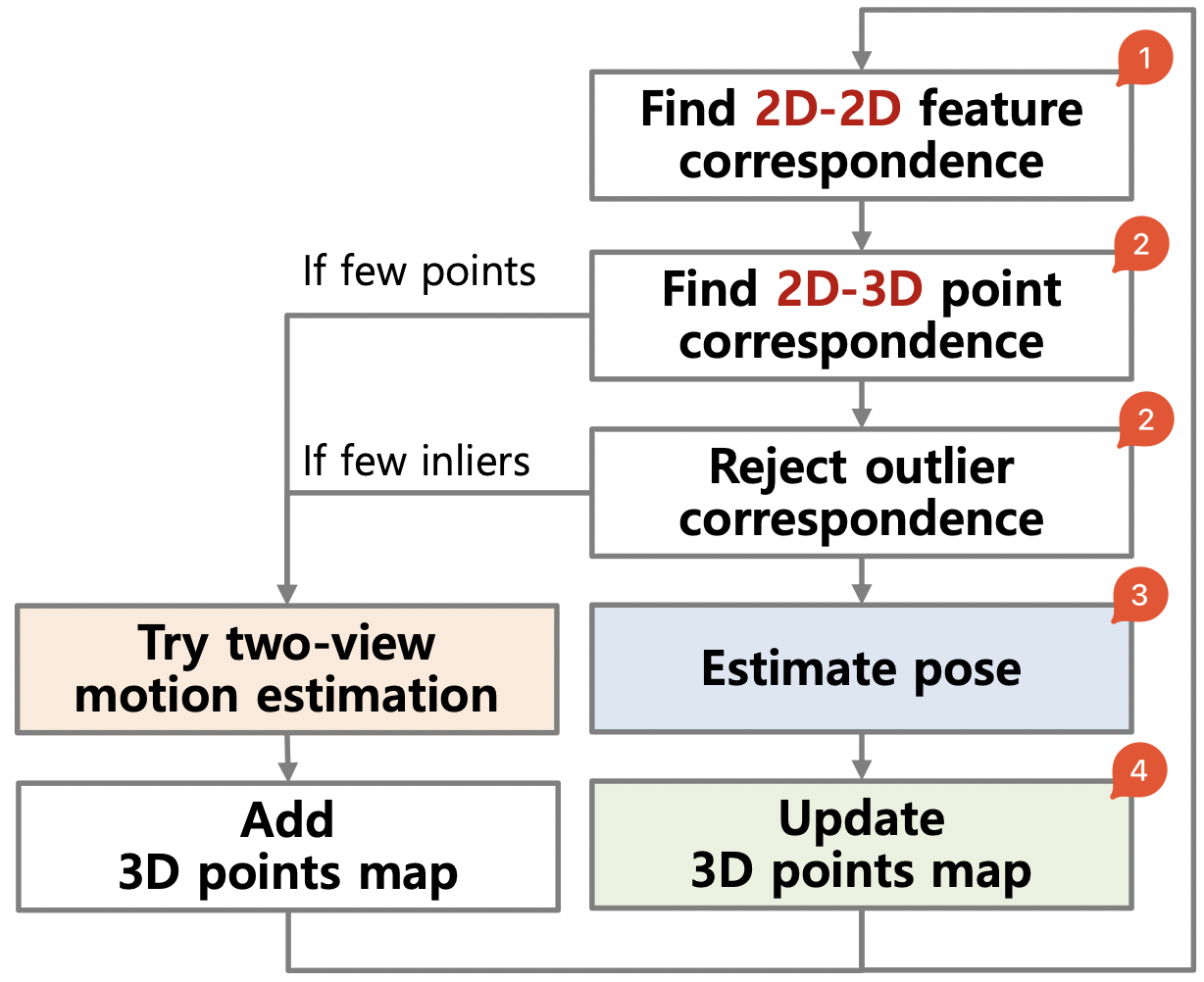

    

    1. Find 2D-2D feature correspondence

       • Feature

         → Good-Feature-to-Track [Shi94_CVPR] with bucketing to distribute features

       • Correspondence

         → Lucas-Kanade optical flow [Lucas81_IJCAI]

    2. Find 2D-3D point correspondence & Reject outlier correspondence
       • Adaptive MSAC
       • Iterative PnP algorithm (3-point algorithm)

       • Error measure

         → Projection error

    3. Estimate pose
       • Iterative PnP algorithm
       • Scale-from-ground with asymmetric kernels [Choi13_URAI]
    4. Updat 3D points map
       • Bundle adjustment over last $K$ keyframes Reprojection error with Cauchy loss function

---

본 포스트는 최성록 교수님의 An Inviation to 3D Vision 자료를 정리한 것입니다.