Dense Reconstruction

Dense Reconstruction

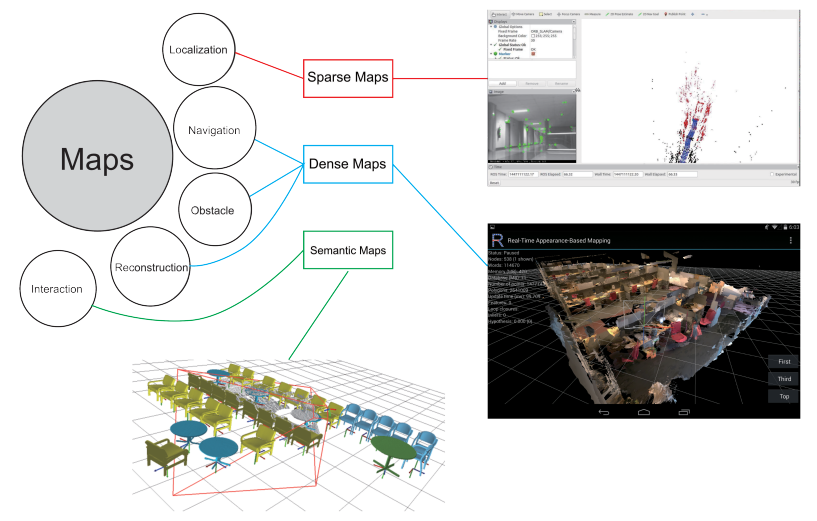
Different type of maps

• 각 카메라들은 과정을 통해 각 픽셀의 거리를 알 수 있음
  • Monocular Camera: 카메라 모션을 통해 triangulation으로 깊이를 추정
  • Stereo Camera: 양안의 disparity를 통해 깊이를 추정
  • RGB-D Camera: depth센서를 통한 깊이 추정

Monocular Dense Reconstruction

Epipolar Line Search and Block Matching

---

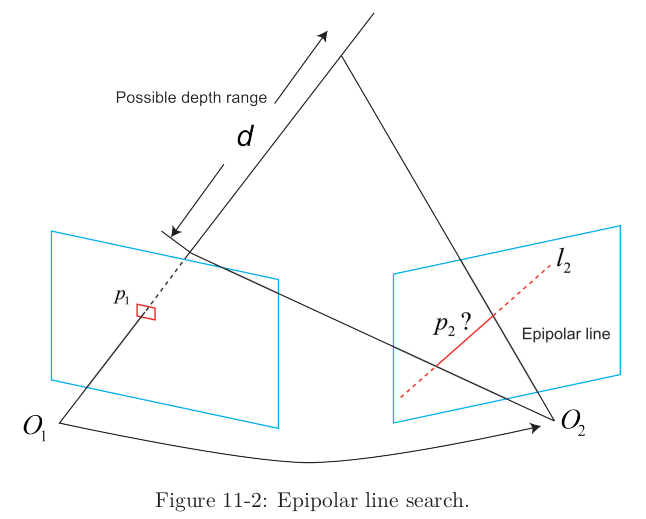
• monocular camera에서 depth 추정 방법
  1. feature 추출
  2. descriptor 기반의 feature들 사이의 matching 수행

  3. 다른 각도의 observations를 통해 triangulation 수행

     → 목표: 다음 frame에서 $p_1$ 지점은 epipolar line라인에서 어느 지점($p_2$)일까?

• Question: epipolar line에 $p_1$과 비슷한 점이 많을 경우 어떤 점을 $p_2$로 결정할 것인가?
  • Solution: Block Matching
    • $p_1$ 주위의 $w \times w$의 작은 블록을 취한 다음, pipolar line 상에 같은 크기의 많은 블록을 비교
    • 한 픽셀의 grayscale invariance에 강해짐

  • 블록과 블록의 차이 계산 방법들 (블럭 유사도 측정)

    

    

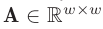
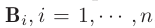
    → $\bold{A}$: $p_1$ 주변의 블록 / $\bold{B}$: epipolar line상의 $n$개의 작은 블록

    → 이미지가 유사하면 0, 다르면 1에 가까워짐

    1. SAD (Sum of Absolute Difference)

       

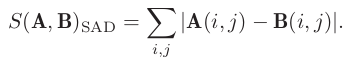
    2. SSD (Sum of Squared Distance), not solid state drive

       

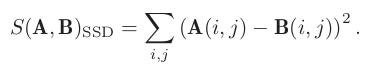
    3. NCC (Normalized Cross Correlation)

       

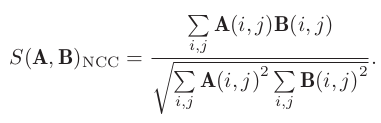
  • epipolar line에서 $\bold{A}$와 $\bold{B}_i$ 사이의 유사성 척도 계산 (NCC를 사용한다고 가정)
    • 결과는 non-convex function이며, 많은 peak들이 있음
    • matching point $p_2$(정답)은 단 하나임
    • 이와 같은 이유로 depth는 단일 값이 아니라 확률분포를 따라야하며, 다른 이미지의 epipolar line들을 찾으면서 depth distribution을 업데이트해야 함 (⇒ depth filter)

    

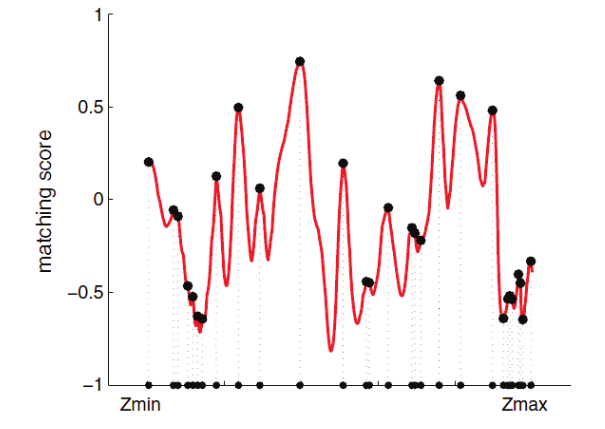
    Matching score along with the epipolar line

Gaussian Depth Filters

---

• 픽셀 깊이의 추정 문제 solution

  • 대안1: 비선형 최적화

    → 이미 frontend에서 많은 계산량을 차지하고 있으므로 pass

  • 대안2: 필터

    → 계산량이 상대적으로 적음

• 유도 과정

  1. 픽셀의 깊이 $d$를 아래와 같이 가우시안 분포를 따른다고 가정

     

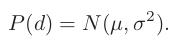
  2. 새로운 데이터를 관측(obs)하였을 때의 깊이 $d_{\mathrm{obs}}$도 마찬가지로 정의하면,

     

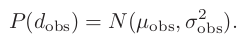
  3. 두 분포에 대한 결합을 정의하면

     → 가우시안 분포의 곱도 가우시안 분포

     → 새로운 관측을 바탕으로 기존 $d$의 분포를 갱신

     

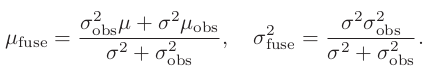
     ⇒ 그렇다면 $\sigma_\mathrm{obs}$는 어떻게 구할 것인가?

     1. epipolar line 탐색과 블록 매칭을 통해, 현재 프레임에서 참조 프레임의 픽셀의 투영 위치를 결정한다고 가정하면 아래 그림과 같이 표현 가능

        → 기하학적 관계로 인한 불확실성만 고려

        

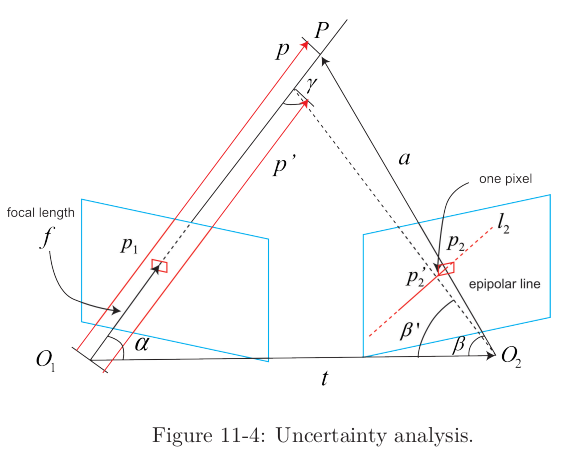
     2. 위 그림에 대한 기하학적 관계를 수식으로 표현하면,

        

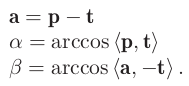
     3. block matching을 수행하기 위해, $p_2$를 이동시키는 것은 $\beta$의 변화를 유발하게 되고, 그에 따라 $\beta’$는

        

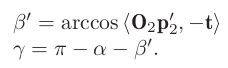
     4. sin 법칙을 통해 단일 픽셀로부터 오는 불확실성 depth $\bold{p’}$를 구하면,

        

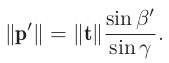
     5. epipolar line상의 block matching에 픽셀 오류가 하나만 있다고 가정하면,

        

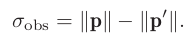
• 픽셀의 depth 추정과정 정리
  1. 모든 픽셀의 depth는 가우시안 분포를 따른다고 가정
  2. 새로운 이미지가 들어오면, 투영 점 위치는 epipolar search와 block matching에 의해 결정
  3. 기하학적 관계를 기반으로 삼각 측량 후의 depth와 uncertainty를 계산
  4. 현재 관측치와 이전 추정 값을 통합 (수렴하면 계산이 중지되고, 그렇지 않으면 2 단계로 돌아감)

Discussion

---

• Pixel Gradients
  • depth의 정확성은 block matching의 결과에 직결됨
    • 이미지 블록이 흑색이나 백색 뿐이거나 유효한 정보가 부족할 경우, matching이 잘 안됨
    • 이 문제는 단안뿐만 아니라 양안 카메라에서도 나타남

    • 아래 오른쪽 그림의 프린터처럼 균일한 흰색의 경우, 왼쪽 결과처럼 부정확한 depth 추정

      

  • pixel gradients와 epipolar line 사이의 각도가 클 때, epipolar line 일치의 불확실성이 큼
    • 각도가 작으면 일치의 불확실성이 작음

    • 극단적인 예 2가지

      

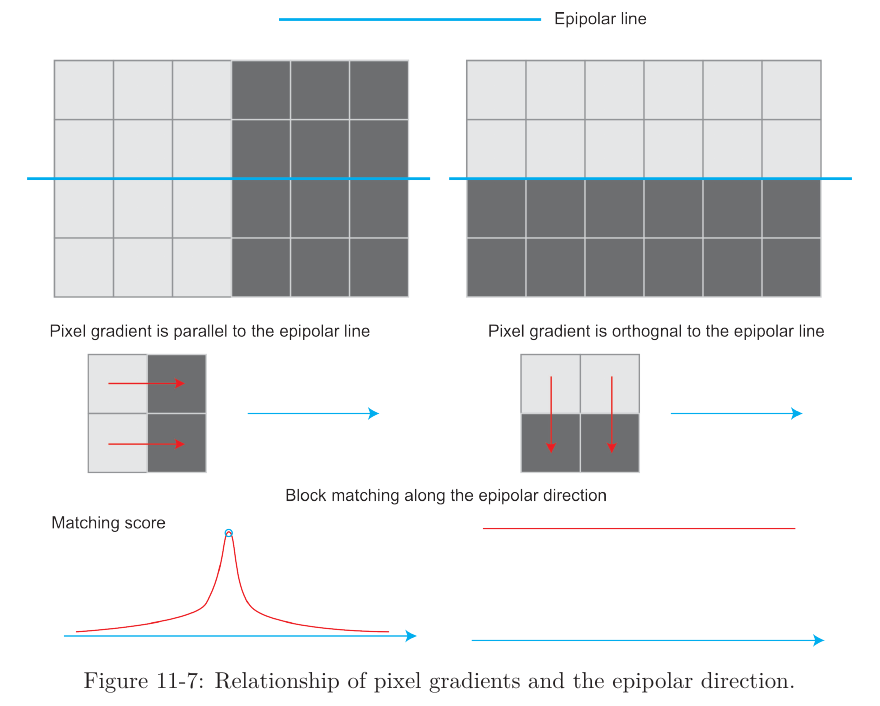
      1. pixel gradients가 epipolar line과 평행한 경우

         → matching point를 정확하게 결정할 수 있음

      2. pixel gradients가 epipolar line과 수직인 경우

         → 명백한 gradients를 가지고 있다고 하더라도, 두 매칭각도가 완전히 동일하므로 효과적인 매칭이 되지 않음

• Inverse Depth Filter
  • depth의 추정 값이 가우시안 분포를 따른다고 가정했을 때의 문제점

    1. 측정 가능한 최소 depth 보다 가까운 거리를 측정할 경우

       → 가우시안 분포의 대칭 모양을 따르지 않게 됨

    2. 야외의 경우 매우 멀리 떨어져있거나 심지어는 무한대인 지점이 있음

       → 초기 값에서 이런 points들을 다루는 것은 힘듦

  • solution: inverse depth
    • 추정된 depth 값을 inverse시킨 $d^{-1}$이 가우시안 분포에 더욱 효과적임
• Pre-transform the Image
  • block matching을 수행하기전, image와 image사이에 transform을 수행하는 전처리 과정을 의미
    • 카메라가 크게 회전했을 때, 이전 frame과 현재 frame의 상관관계에 문제가 생기는 것을 방지
  • 참조 frame과 현재 frame의 모션을 고려해야 함

    1. 참조 frame의 한 점 $\bold{P}_R$은 실제 3차원 world 포인트 좌표 $\bold{P}_W$와 아래와 같은 관계를 갖음

       

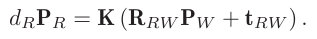
    2. 현재 frame의 한 점 $\bold{P}_C$도 $\bold{P}_W$와 아래와 같은 관계를 갖음

       

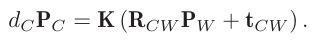
    3. $\bold{P}_W$를 제거하기 위해 대입하면 아래와 같은 관계식이 나옴

       → $d_{R},\bold{P}_R$을 알고 있으면, $\bold{P}_C$를 계산 할 수 있음

       

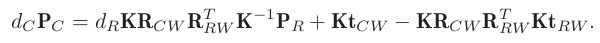
    4. $\bold{P}_R$의 증분 $\mathrm{d}u,\mathrm{d}v$이 주어졌을 때, 그에 따른 $\bold{P}_C$의 $\mathrm{d}u_C,\mathrm{d}v_C$를 구할 수 있고, 선형 관계를 affine 변환 꼴로 표현하면,

       

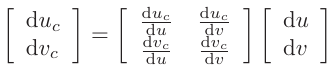
  • 위 affine 변환 수행 후, block matching을 수행할 경우 더욱 좋은 결과를 얻을 수 있음
• Parallel Computing
  • epipolar line search를 수행할 때, 이중 루프로 모든 픽셀을 순회하는 것은 비효율적
  • solution
    • 각 픽셀에 대해 모든 연산들은 독립적이므로 thread를 이용하여 처리
    • GPU을 이용하여 병렬 처리
• Other Improvements

  • 각 픽셀은 독립적으로 계산되므로, 한 픽셀의 depth가 작고 인접한 다음 픽셀의 depth는 매우 클 때 depth map이 smooth하지 않음

    ⇒ Solution: 인접한 픽셀의 depth 값 차가 클 경우, regularization term을 추가

  • occlusion, lighting, motion blur등으로 발생하는 outlier로 인한 mismatch

    ⇒ Solution1: NCC가 특정 값 보다 크면 일치로 판단하고, 작으면 불일치로 판단

    ⇒ Solution2: uniform-Gaussian mixture model 적용

RGB-D Dense Reconstruction

• 포인트 클라우드들의 효율적인 처리
  1. 초기 생성 시: 유효하지 않은 depth를 가진 point들 제거
  2. statistical filter: 가장 가까운 N 점에서 각 점의 거리 값 분포를 계산하여, 평균 거리가 너무 큰 점을 제거하는 방식으로 outlier 제거

  3. voxel filter: 중첩 영역에는 많은 수의 밀집된 점을 다운샘플링

     

Octo-Mapping

---

• 3차원 공간의 데이터 표현 방식

  

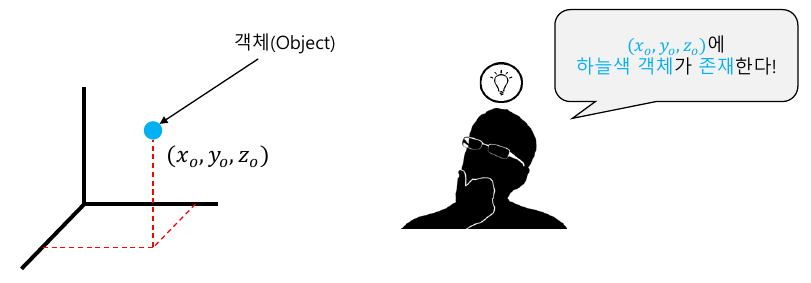
  • 어떤 객체의 정보를 나타내기 위해서는 객체의 존재 여부와 객체가 어디에 존재하는지를 알아야 함

    → 기준 좌표계(or 공간)에 대한 정의가 필요한 이유

    

  • 그렇다면 3차원 박스에는 몇 개의 Point가 존재할 수 있을까?

    

  • 정답은 무수히 많다
    • 따라서 일정한 부피를 갖는 기준공간이 필요 ⇒ 복셀(Voxel)

    • 어떤 3차원 공간을 Voxel 기준으로 표현할 수 있음

      

  • Voxel을 활용하면 데이터의 공간을 절약할 수 있음

    

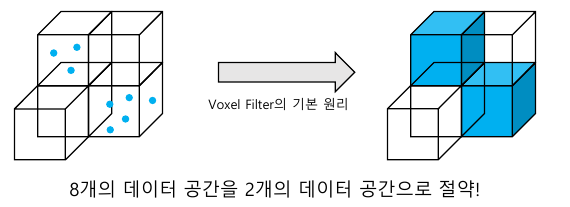
  • 정리
    • 픽셀(Pixel): 2D 공간의 한 점을 정의한 그래픽 정보
    • 복셀(Voxel): 3D 공간의 한 점을 정의한 그래픽 정보

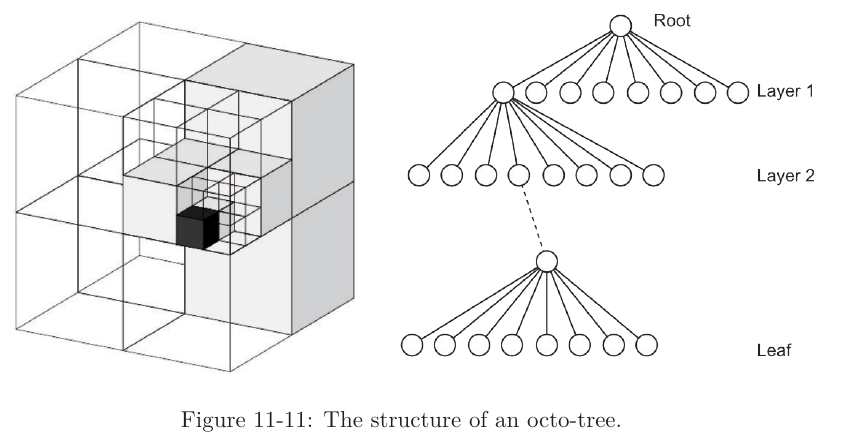
    • Octree: Voxel의 개념을 이용하여 3차원 공간에 데이터를 표현하는 방법

      ⇒ 예

      1. 부모 노드에 표현하고자하는 객체가 있을 경우, 부모노드가 8개의 자식노드 생성
      2. 생성한 자식 노드 중, 객체를 포함하는 노드가 또 다른 자식노드를 만듦
      3. 더 이상 자식 노드를 생성할 필요가 없을 때까지 이를 반복

      

• Octree의 확률적 데이터 표현 방식

  • 사람의 눈(센서)는 100% 정확하지 않음

    

  • 또한, 사람마다 객체(데이터)를 판단하는 기준이 다름

    → 객체의 정보를 취득하는 센서는, 불확실한 데이터를 취득할 가능성이 있음

    

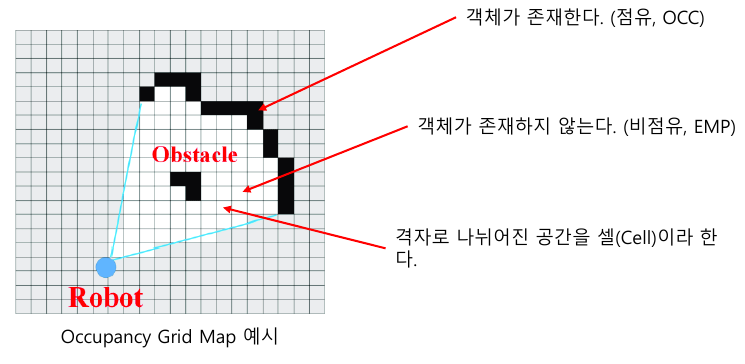
  • 이러한 센서의 불확실성을 확률적 모델링하여 객체의 존재 여부를 표현하면

    

  • 데이터표현 방식

    • 가정

      → 센서로부터 데이터를 지속적으로 취득하고, octree의 노드는 점유 여부에 대한 정보를 저장

    • 목표

      → 이전까지 취득한 데이터를 활용하여, 객체(장애물 등) 정보를 동적으로 모델링

    • 간단한 솔루션
      1. 모든 cell의 확률 값 $\mathrm{P(x)}$를 0.5로 정의

      2. 객체가 해당 cell에 존재하면 $\mathrm{P(x)}$의 값을 증가

         → 단순증가: 예) $\mathrm{P(x)}+=0.1$

      3. 반대로, 객체가 해당 cell에 존재하지 않으면 $\mathrm{P(x)}$의 값을 감소

         → 단순감소: 예) $\mathrm{P(x)}-=0.1$문제점

    • 문제점: 시간이 지남에 따라, $\mathrm{P(x)}$가 [0, 1]의 값을 벗어날 수 있음

    • 해결책: $\mathrm{P(x)}$에 $\mathrm{log}$를 취해 문제를 해결

      → logit transform 사용

      

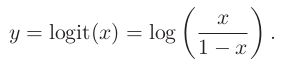
      → 역함수의 경우

      

      → $y$가 $-\infty$에서 $+\infty$로 변하면, $x$는 0에서 1로 변함 ($y$가 0이면, $x$는 0.5)

그림 참고 (SLAM KR)

TSDF and RGB-D Fusion Series

---

• Truncation Signed Distance Function (TSDF)
  • 목적: 잡음과 불확실성을 내포한 깊이 영상 으로부터 3차원 공간 표면을 효과적으로 표현
  • 전체 공간을 일정한 크기의 정육면체 복셀(voxel)들로 구성된 커다란 하나의 큐브(cube)로 표현
  • 각 복셀에는 물체 표면과의 거리를 나타내는 TSDF값과 그 값의 신뢰도를 나타 내는 가중치(weight) 를 함께 저장하는 방식
    • 표면 앞 →양수 / 표면 뒤 → 음수
    • zero-crossing point는 물체의 표면

    

Stereo Dense Reconstruction

Data Structure

---

• frame: 이미지의 단위
• feature: 2D pixel 상의 특징
• landmark: 삼각측량 법으로 얻어진 3D position

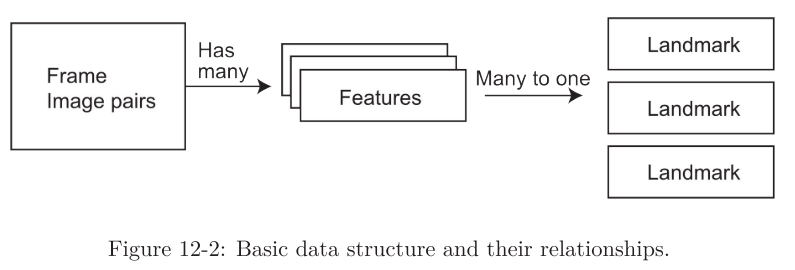
Pipeline

---

• frontend
  • 이미지의 특징 추출
  • optical flow tracking 또는 feature matching를 통해 프레임의 위치를 계산
  • 필요한 경우 새 feature point를 추가하고 삼각측량 수행
  • 프런트엔드 처리 결과는 백엔드 최적화의 초기 값으로 사용
    1. “initialization” state

    → optical flow matching에 따라 triangulation 수행

    → 성공 시 초기 map 생성

  1. “normal tracking” state

     → 이전~현재 프레임까지의 optical flow를 계산하고, 결과를 바탕으로 영상 포즈를 추정

     → optical flow 계산 리소스를 절약하기 위해, stereo에서는 한 쪽 이미지에만 사용

  2. “tracking lost” state

     → tracked feature가 threshold 보다 작을 경우 발생

     1. 새로운 feature point 추출
     2. triangulation을 통해 새로운 landmark 생성
     3. 지도에 새 key frame과 landmark 를 추가하고, backend optimization을 trigger
     4. 그래도 tracking lost일 경우, frontend를 초기화
• backend
  • 느린 스레드
  • 키 프레임과 랜드마크 포인트를 통해 pose 최적화 수행 후, 결과를 반환
  • 새로운 데이터에 대해, 최적화 후 map scale 조절 등을 수행

Etc.

---

• projection 및 intrinsic와 extrinsic를 처리할 camera class
• configuration file을 관리할 class
• 데이터셋 및 이미지를 읽을 class
• visualization module